A. Pertidaksamaan Pecahan
1. Bentuk Baku
Dengan  dan
dan  merupakan fungsi-fungsi variabel x dan
merupakan fungsi-fungsi variabel x dan  .
.
2. Sifat-Sifat Pertidaksamaan Pecahan
a.  .
.
b.  .
.
c.  .
.
d.  .
.
3. Metode Penyelesaian Pertidaksamaan Pecahan
a. Tenukan pembuat 0 bagian pembilang dan penyebut dari bentuk pecahan  , yaitu
, yaitu 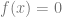 dan
dan  .
.
b. Gambarlah nilai-nilai 0 itu pada diagram garis bilangan sehingga diperoleh interval-interval.
c. Tentukan tanda-tanda interval (positif atau negatif) dengan cara mensubstitusikan nilai-nilai uji yang berada dalam masing-masing interval.
d. Tetapkan interval yang memenuhi, dan tulislah himpunan penyelesaiannya.
Dalam menentukan interval yang memenuhi itu, perlu diingat adanya syarat bahwa bagian penyebut tidak boleh sama dengan 0 atau  .
.
B. Pertidaksamaan Bentuk Akar
1. Bentuk Umum
a. 
b. 
c. 
d. 
e. 
f. 
g. 
h. 
Dengan syarat  ,
,  dan
dan  ,
,  dan
dan  (p dan
(p dan  serta
serta  adalah bilangan real positif atau 0).
adalah bilangan real positif atau 0).
2. Metode Penyelesaian Pertidaksamaan Bentuk Akar
a. Kuadratkan kedua ruas, kemudian selesaikan.
b. Persyaratan fungsi yang berada di dalam akar harus bernilai positif atau 0.
c. Tentukan interval pada langkah a dan b.
d. Irisan antara interval langkah a dan b merupakan penyelesaiannya.
C. Pertidaksamaan Nilai Mutlak
1. Nilai Mutlak
Nilai mutlak dari suatu bilangan real x (|x|) adalah nilai tak negatif dari bilangan real x tersebut.
Nilai mutlak dari suatu bilangan real x, ditulis |x|. Didefinisikan sebagai berikut:
2. Pertidaksamaan Nilai Mutlak
Pertidaksamaan nilai mutlak adalah suatu pertidaksamaan yang variabelnya berada di dalam tanda mutlak.
Untuk k, x, y, a, b, m, n ∈ R dan k > 0, maka:
a. 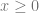 .
.
b. Jika  , maka
, maka  .
.
c.  .
.
d.  .
.
e. 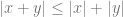 .
.
f. Untuk  dan
dan  , berlaku:
, berlaku:
1. 
2. 
g. Untuk  dan
dan  , berlaku:
, berlaku:
1. 
2. 
h. Untuk  dan
dan  , berlaku:
, berlaku:
1. 
2. 
i. 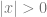 dipenuhi oleh x ∈ R, dan
dipenuhi oleh x ∈ R, dan  .
.
j.  hanya dipenuhi oleh
hanya dipenuhi oleh  .
.
k.  tidak ada nilai x ∈ R yang memenuhi.
tidak ada nilai x ∈ R yang memenuhi.
l.  dan
dan  dipenuhi oleh x ∈ R.
dipenuhi oleh x ∈ R.












0 comments:
Post a Comment